1 Answer

Jimoc · Answer 1 · 2023-12-09T02:31:14+0000

We are given the following equation

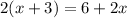
$2(x+3)=6+2x_{}$

We are asked to determine if the above equation has "One Solution", "No Solutions", or "Infinite Many Solutions"

Let us first open the brackets on the left side of the equation

$\begin{gathered} 2(x+3)=6+2x_{} \\ 2x+6=6+2x_{} \end{gathered}$

As you can see the L.H.S and R.H.S of the equation is the same.

Whenever an equation has L.H.S = R.H.S then we get "Infinite Many Solutions"

Let us verify if there are many such solutions

Let us substitute x = 1

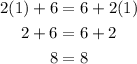
$\begin{gathered} 2(1)+6=6+2(1) \\ 2+6=6+2_{} \\ 8=8 \end{gathered}$

As you can see the equation is satisfied.

Now Let us substitute x = 2

$\begin{gathered} 2(2)+6=6+2(2) \\ 4+6=6+4 \\ 10=10 \end{gathered}$

No matter what value you substitute, the equation will always be

Please log in or register to add a comment.