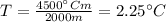Question

the water temperature of the ocean varies inversely as the water's depth. at a depth of 1000 meters, the water temperature is 4.5 Celsius. what is the water temperature at a depth of 2000 meters? at a depth of 2000 meters, the water temperature of the ocean is ____ celsius.

Answer 1

Since the water temperature and water's depth are inversely proportional we can set the following equation:

`T=(k)/(d)`

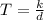
where k is the proportionality constant. On the other hand, we know that

`4.5^(\circ)C^{}=(k)/(1000m)`

Solving for k we get:

`k=4.5^(\circ)C\cdot1000m=4500^(\circ)Cm`

Then at a depth of 2000 meters, the temperature is:

`T=(4500^(\circ)Cm)/(2000m)=2.25^(\circ)C`