We are given the following equation:
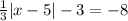
we are told to "isolate" the absolute value. This means that we need to solve for the expression inside the absolute value. To do that we will first add 3 to both sides:

Solving the operations:
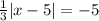
Now we will multiply both sides by 3:
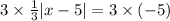
Solving the operations:

Now that the expression in the absolute value is on the right side of the equation we have isolated it.
Now we proceed to solve the equation. To do that we need to separate the absolute value. Any expression inside an absolute value has two possible forms, these are:
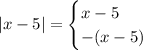
This means that the absolute value is decomposed into a positive and a negative expression.
But since on the right side we have a negative number, an expression in absolute value can't be equal to a negative number, therefore, there are no solutions to this equation. If the number on the right side was positive then we would decompose the absolute value as shown and solve each for "x".