Question

Bill Baxter has $25,000 to invest for a year. He can lend it to his sister, who has agreed to pay 10% simple interest for the year. Or, he can invest it in a retirement plan expected to pay 6% compounded quarterly for a year. How much additional interest would the simple interest loan to his sister generate?

Answer 1

Given:

`\begin{gathered} P=\text{ \$25,000} \\ R=10\text{ \%} \\ T=1\text{year} \end{gathered}`

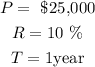
To get the interest lent to his sister at 10% simple interest;

Using the simple interest formula;

`\begin{gathered} I=\frac{\text{PTR}}{100} \\ I=(25000*1*10)/(100) \\ I=\text{ \$2500} \end{gathered}`

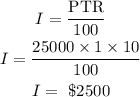
Hence, the sister will pay back $2500 interest for the money lent.

To get the interest gotten if he invests in a retirement plan at 6% compounded quarterly for a year;

Using the compound interest formula;

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ P=\text{ \$25000} \\ r=6\text{ \%=}(6)/(100)=0.06 \\ n=4\text{ (compounded quarterly)} \\ t=1\text{year} \\ \\ A=25000(1+(0.06)/(4))^(4*1) \\ A=25000(1+0.015)^4 \\ A=25000(1.015)^4 \\ A=25000*1.015^4 \\ A=\text{ \$26,534.09} \end{gathered}`

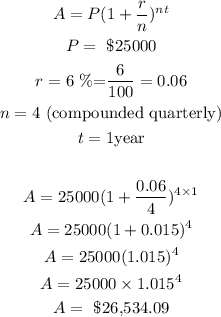
To get the interest made from the retirement plan,

`\begin{gathered} \text{Amount}=\text{principal+interest} \\ Interest=amount-pri\text{ncipal} \\ I=26534.09-25000 \\ I=\text{ \$1534.09} \end{gathered}`

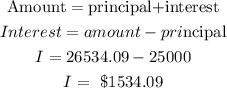
Hence, the interest made from the retirement plan compounded quarterly for a year is $1534.09

Thus, the additional interest the simple interest loan to his sister will generate is;

`\begin{gathered} \text{Additional interest = 2500-1534.09} \\ \text{Additional interest =\$965.91} \end{gathered}`

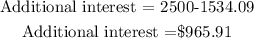
Therefore, the additional interest the simple interest loan to his sister will generate is $965.91