The x-component of the net force on
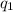 is approximately
is approximately
 N (rounded to four decimal places), with the negative sign indicating that the net force is in the negative x-direction.
N (rounded to four decimal places), with the negative sign indicating that the net force is in the negative x-direction.
To find the x-component of the net force on
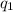 due to the charges
due to the charges
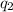 and
and
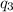 , we can use Coulomb's law, which states that the force between two charges is:
, we can use Coulomb's law, which states that the force between two charges is:
![\[ F = k (|q_1 q_2|)/(r^2) \]](https://img.qammunity.org/2023/formulas/physics/college/wsqtoevyaos0x3o40pjmj66gvubrdc0egj.png)
where:
- F is the magnitude of the force between the charges,
- k is Coulomb's constant
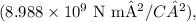
-
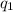 and
and
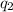 are the magnitudes of the charges,
are the magnitudes of the charges,
- r is the distance between the charges.
The x-component of the force can be found by multiplying the force by the cosine of the angle with respect to the x-axis.
We have three charges:
-
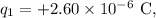
-
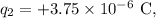
-
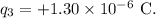
The distances are:
- Between
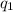 and
and
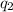 :
:
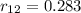 m,
m,
- Between
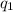 and
and
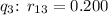 m (since
m (since
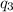 is directly on the x-axis from
is directly on the x-axis from
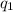 , the force between
, the force between
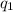 and
and
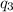 will only have an x-component).
will only have an x-component).
The angle between
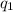 and
and
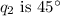 , which means the x-component of the force due to q2 will involve the cosine of
, which means the x-component of the force due to q2 will involve the cosine of
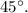
Let's calculate the x-component of the force on q1 due to q2 first, and then add the force due to q3 (which lies on the x-axis, so its entire force is an x-component).
The force from q2 on q1 is repulsive and to the left (negative x-direction), and the force from q3 on q1 is also repulsive and to the right (positive x-direction) because like charges repel.