The grain silo is a compound shape of a cylinder and a hemispherical top
The volume of the grain that could completely fill the silo is equivalent to the volume of the silo
The volume of the silo = Volume of the cylindrical body + Volume of the hemispherical top
The volume of the Cylindrical body is calculated thus:
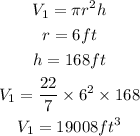
The volume of the Hemispherical top is calculated thus:
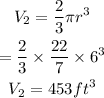
Hence, the volume of the silo is:
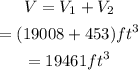
The answer is 19,461 ft³