Given the expression:
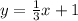
To find the order pairs that are the solution of this equation, substitute x and find y. Then verify if the y found is the same as the y in the ordered pair.
a) (-6, -1).
Substituting x by -6:
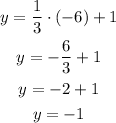
The solution is (-6, -1) and the ordered pair is (-6, -1). Thus (-6, -1) is a solution.
b) (9, 4).

The solution is (9, 4) and the ordered pair is (9, 4). Thus (9, 4) is a solution.
c) (-3, 0).
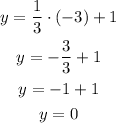
The solution is (-3, 0) and the ordered pair is (-3, 0). Thus (-3, 0) is a solution.
In summary,
The order pairs (-6, -1), (9, 4) and (-3, 0) are solutions of the equation.