Given that the function is
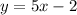
with the domain given below as
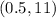
The range is the set of values generated by the evaluation of the function for the set of domain values.
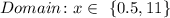
The range of the function will be
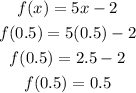
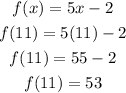
Hence,
The range of the function y=5x-2 is
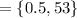
Therefore,
The final answer is OPTION D