Let:
P1 = Investment #1
P2 = Investment #2
r1 = Rate #1
r2 = Rate #2
I1 = Income 1
I2 = Income 2
The 2 investment produce an annual income of $3000, so:
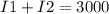
One investment yields 9% per year, while the other yields 6% per year:
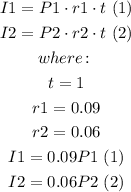
Two Investments totaling $47,500 so:
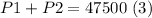
Add (1) and (2):
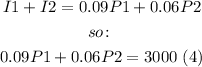
From (4) solve for P1:
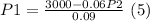
Replace (5) into (3):
![undefined]()