Question

An initial population of 620 birds increases at an annual rate of 16% write an exponential function to model the bird population what will the approximate population be after four years?

Answer 1

approximate

`y=620(1.16)^x\rightarrow\text{ model}`

after 4 years: 1123 birds

Step-by-step explanation

o calculate exponential growth, use the formula:

`\begin{gathered} y=a(1+b)^x \\ where\text{ a is the initial population} \\ b\text{ is the rate ( in decimal)} \\ x\text{ is the time ( in years)s} \\ y\text{ is the population after x years} \end{gathered}`

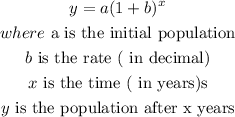
so

Step 1

Let

`\begin{gathered} \text{ Initial value= a= 620} \\ \text{rate = 16 \%= }\frac{16\text{ }}{100}=0.16 \\ \text{time = 4 years} \end{gathered}`

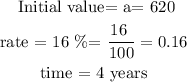
now replace

`\begin{gathered} y=a(1+b)^x \\ y=620(1+0.16)^3 \\ y=620(1+0.16)^x \\ y=620(1.16)^x\rightarrow\text{ model} \end{gathered}`

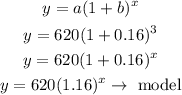
Step 2

now, evaluate for

x= 4 ( 4 years)

`\begin{gathered} y=620(1.16)^x\rightarrow\text{ model} \\ y=620(1.16)^4 \\ y=620(1.8106) \\ y=1122.5964 \\ \text{rounded} \\ y=1123 \end{gathered}`

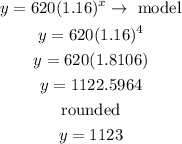
therefore

the aproxximate population after 4 years is 1123 birds

I hope this helps you