Question

4. Jon orders 4 shirts for $35. Later he orders 12 shirts for $95. Because he is anew customer, the shipping cost is a reduced value for his first five orders.Predict the cost of 10 shirts on his third order.

Answer 1

we are given the cost for 4 shirt s and for 12 shirts. Assuming that the shipping cost is constant, we can model the cost of the shirts as a linear equation. So, we want to find an equation of the form

`y=mx+b`

where m is the slope of the line and b is the y-intercept.

Using the given information, we can wirte the following points (4,35) and (12,95). We will use this points to find the value of b and m.

Recall that the slopé of a line that passes through points (a,b) and (c,d) is described by the formula

`m=\frac{d\text{ -b}}{c\text{ -a}}=\frac{b\text{ -d}}{a\text{ -c}}`

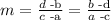
in our case, we have a=4, b=35, c=12 and d=95. So we get

`m=\frac{95\text{ -35}}{12\text{ -4}}=(60)/(8)=(30)/(4)=(15)/(2)=7.5`

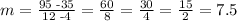
So, so far we have the equation

`y=7.5x+b`

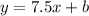
To find the value of b, we will use tghe fact that, as the line should pass through the point (4,35), this means that if we replace x by 4, we should replace y by 35. So we have that

`35=7.5\cdot4+b=30+b`

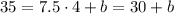
so if we subtract 30 on both sides, we get

`b=35\text{ -30=5}`

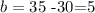
so the line equation would be

`y=7.5x+5`

Now, we want to find the price for 10 tshirts. So we simply replace x=10 to find

`y=7.5\cdot10+5=75+5=80`

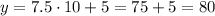
so the price of 10 tshirts is 80