Question

A fair die is rolled five times. A 5 is considered success while all other outcomes are failures. Find the probability of 0 successes out of 5 rolls.

Answer 1

When a probability deal with obtaining succes a number of times, it is Binomial probability distribution.

The formula for Bimomial probability distribution is

`\begin{gathered} p(x)=^nC_xp^xq^(n-x) \\ \text{where } \\ n=\text{ Number of trials} \\ p=probability\text{ of success} \\ q=1-p \\ x=total\text{ number of successes} \end{gathered}`

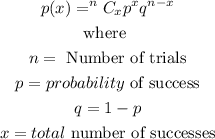
For the given question, we have

`\begin{gathered} n=5,x=0 \\ p=(1)/(6),q=1-(1)/(6)=(5)/(6) \end{gathered}`

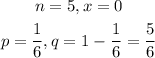
A die has six total outcome, the probability of obtaining a number out of six is 1/6, this account for the value of p above.

stituting the value into the formula, we have

`\begin{gathered} p(x)=^5C_0((1)/(6))^0((5)/(6))^5 \\ \text{Recall that }^5C_0=1,\text{ then} \\ p(x)=1*1*((5)/(6))^5 \\ P(x)=(3125)/(7776)=0.4019 \end{gathered}`

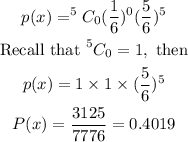
Therefore

The probability of 0 successes out of 5 rolls when a die is rolled five times and a 5 is considered success is 0.4019.

Answer = 0.4019