Given,
The mass of the rock, m=20 kg
The height of the cliff, h=100 m
A)
When the rock is at the height of h meters on the cliff at rest, it possesses only potential energy. As it starts to fall, it slowly loses its potential energy and gains kinetic energy. Just before it hits the ground, all its potential energy is converted into kinetic energy.
Thus, the kinetic energy of the rock just before it hits the ground is equal to its potential energy when it was on the cliff.
Thus, the equation to find out the kinetic energy of the rock the instant before it strikes the ground is,
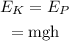
Where:
• E_K is the kinetic energy of the rock just before it hits the ground.
,
• E_P is the potential energy of the rock when it is on the cliff.
,
• g is the acceleration due to gravity.
On substituting the known values,

Therefore the kinetic energy of the rock the instant before it strikes the ground is 19.6 kJ.
B)
The kinetic energy of the rock is also given by,
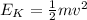
Where v is the velocity of the rock.
The speed of the rock as it strikes the ground can be calculated by substituting the known values in the above equation.
Thus,
![\begin{gathered} 19.6*10^3=(1)/(2)*20* v^2 \\ v^2=(2*19.6*10^3)/(20) \\ v=\sqrt[]{1960} \\ =44.27\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/5oeqdbzhv2oor296vxinjzpy63mclt2bgl.png)
Therefore the speed of the rock as it strikes the ground is 44.27 m/s