Given the word problem, we can deduce the following information:
1. The ratio of the two complementary angles is 3:7.
To determine the measures of both angles, we must note first that complementary angles are two angles whose measures add up to 90°. So our equation would be:
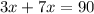
We simplify the equation above:
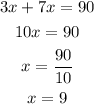
We plug in x=9 into 3x to get the first angle:
Angle 1 = 3x = 3(9) = 27
Then, we plug in x=9 into 7x to get Angle 2:
Angle 2= 7x=7(9)=63
Therefore, the measures of both angles are 27° and 63°.