Question

A person draws a card from a hat. Each card is one color, with the following probabilities of being drawn: 1/25 for yellow, 1/15 for black, 1/20 for red, and 1/10 for purple. What is the probability of pulling a purple or black card, written as a reduced fraction?

Answer 1

Step-by-step explanation

From the statement, we have a hat with cards and the following probabilities for drawing each of the cards:

• P(yellow) = 1/25,

,

• P(black) = 1/15,

,

• P(red) = 1/20,

,

• P(purple) = 1/10.

Drawing a purple or a black card car are independent events so the probability of drawing a purple or a black card, so the probability is the sum of the individual probabilities:

`P(\text{purple or black})=P(\text{purple})+P(\text{black})=(1)/(10)+(1)/(15).`

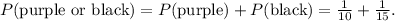
Reducing the fraction, we have:

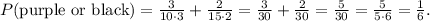
`P(\text{purple or black})=(3)/(10\cdot3)+(2)/(15\cdot2)=(3)/(30)+(2)/(30)=(5)/(30)=(5)/(5\cdot6)=(1)/(6).`Answer

The probability of pulling a purple or black card is 1/6.