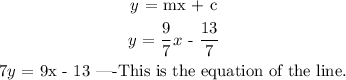Question

write the equation of the line that is perpendicular to the line -7 x - 9y = -35 and contains the points (-4,-7)

Answer 1

When two lines are perpendicular, Their gradients ( slopes ) are m1 x m2 = -1 , we meed to find the second gradient, then use it to find the second intercept to create the second equation of line.

Since the equation of line is y = mx + c

put the equation, -7x - 9y = -35 in the above format

-9y = -35 + 7x

`\begin{gathered} y\text{ = }(-35)/(-9)\text{ + }(7x)/(-9) \\ y\text{ = -}(7x)/(9)\text{ +}(35)/(9) \\ \text{The gradient m1 = -}(7)/(9) \\ m1\text{ x m2 = -1 } \\ so\text{ -}(7)/(9)\text{ x m2 = -1} \\ -7m2\text{ = -9} \\ m2\text{ = }(9)/(7) \end{gathered}`

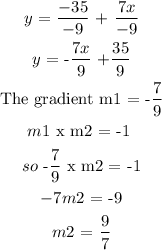
Since the points ( -4, -7 ) are given, and gradient m2 = 9/7. We put it in the equation of line to get the intercept.

`\begin{gathered} y\text{ = mx + c } \\ -7\text{ = }(9)/(7)(\text{ -4 ) + c } \\ -7\text{ = }(-36)/(7)\text{ + c } \\ -7\text{ + }(36)/(7)\text{ = c} \\ \frac{-49\text{ + 36}}{7}\text{ = c } \\ (-13)/(7)\text{ = c} \end{gathered}`

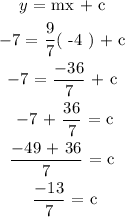
The intercept is - 13/7 and the gradient is 9/7, hence, the equation of line is ...

`\begin{gathered} y\text{ = mx + c } \\ y\text{ = }(9)/(7)x\text{ - }(13)/(7)\text{ } \\ 7y\text{ = 9x - 13 ----This is the equation of the line. } \end{gathered}`