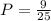Question

Use the bar graph to find the experimental probability of rolling a 2 or 6.

Answer 1

The experimental probability of rolling a 2 or 6 is 0.36

How to find the experimental probability of rolling a 2 or 6.

From the question, we have the following parameters that can be used in our computation:

The bar graph

Where, we have

n(2) = 16

n(6) = 20

Total = 13 + 16 + 15 + 17 + 19 + 20

Total = 100

Using the above as a guide, we have the following:

P(2 or 6) = (16+ 20)/100

Evaluate

P(2 or 6) = 0.36

Hence, the probability is 0.36

Answer 2

Given the bar graph shown in the exercise, you need to remember that the formula for calculating the Experimental Probability is:

`P(event)=\frac{Number\text{ }of\text{ }times\text{ }event\text{ }occurs}{Total\text{ }number\text{ }of\text{ }trials}`

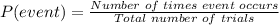
In this case, since you need to find the Experimental Probability of rolling a 2 or 6, you can set up that:

`P=P_2+P_6`

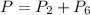
According to the bar graph, the "Times rolled" that corresponds to 2 is 16, and the one that corresponds to 6 is 20 times rolled.

Notice that the sum of the values of "Times rolled" for all the numbers rolled, is:

`Total=13+16+15+17+19+20=100`

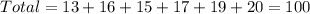
Therefore, you can determine that:

`P=(16)/(100)+(20)/(100)`

Adding the fractions and simplifying, you get:

`\begin{gathered} P=(16+20)/(100) \\ \\ P=(36)/(100) \\ \\ P=(9)/(25) \end{gathered}`

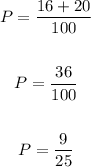
Hence, the answer is:

`P=(9)/(25)`