Evaluate the integral of 4 raised to the power of 3 times x, dx

Question

asked Mar 20, 2023 165k views

1 Answer

JuanGG · Answer 1 · 2023-03-26T13:30:40+0000

We have to evaluate the integral:

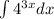
$\int4^(3x)dx$

We start with a substitution:

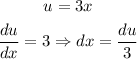
$\begin{gathered} u=3x \\ (du)/(dx)=3\Rightarrow dx=(du)/(3) \end{gathered}$

Then, we can now apply the substitution and then the rule for exponential functions:

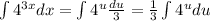
$\int4^(3x)dx=\int4^u(du)/(3)=(1)/(3)\int4^udu$
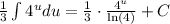
$(1)/(3)\int4^udu=(1)/(3)\cdot(4^u)/(\ln(4))+C$

We can replace back with x and write:

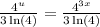
$(4^u)/(3\ln(4))=(4^(3x))/(3\ln(4))$

Then, the solution to the integral is:

$\int4^(3x)dx=(4^(3x))/(3\ln(4))+C$

This result does not match any of the options.

Answer: none of these.