Question

Please help me work through this or at least part, I thought i understood, but i need help!

Answer 1

Step 1:

Write the equation for the distance function:

`v(t)\text{ = -cost + 3sint + 3}`

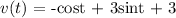
Step 2:

_______________________-___________________________________

Part 1

`\begin{gathered} v(t)\text{ = -cost + 3sint + 3} \\ \\ (ds(t))/(dt)=−cost+3sint+3 \\ \\ ds(t)=(−cost+3sint+3)dt \\ \\ s(t)=\int(−cost+3sint+3)dt \\ \\ s(t)\text{ = -sint - 3cost + 3t + c} \\ \\ s(0)\text{ = -sin\lparen0\rparen - 3cos\lparen0\rparen + 3\lparen0\rparen + c} \\ c\text{ = 3} \end{gathered}`

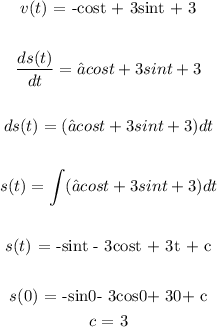
Find s(t), if s(0) = 0

s(t) = -sint - 3cost + 3t + 3

________________________________________________________

Part 2

`\begin{gathered} v(t)\text{ = -cost + 3sint + 3} \\ \\ a(t)\text{ = }(dv(t))/(dt) \\ \\ (dv(t))/(dt)\text{ = sint + 3cost} \\ \\ a(t)\text{ = sint + 3cost} \end{gathered}`

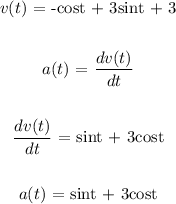
Find a(t)

a(t) = sint + 3cost