Question

10#Suppose that the quarterly sales levels among health care information systems companies are approximately normally distributed with a mean of 12 million dollars and a standard deviation of 1.1 million dollars. One health care information systems company considers a quarter a "failure" if its sales level that quarter is in the bottom 20% of all quarterly sales levels. Determine the sales level (in millions of dollars) that is the cutoff between quarters that are considered "failures" by that company and quarters that are not. Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.

Answer 1

We have the following information from the question:

• Variable: Quarterly sales levels

,

• They are approximately normally distributed

,

• The population's mean is 12 million dollars

,

• The population's standard deviation is 1.1 million dollars

,

• A quarter is a "failure" if its sales level is in the bottom 20% of all quarterly sales levels

And we need to determine:

• The sales level - in millions of dollars - is the cutoff between quarters that are considered "failures" by that company and quarters that are not.

To find that, we can proceed as follows:

1. We can use the z-scores, that is, we have to use the cumulative standard normal distribution in which the variable Z follows a normal distribution with a mean equal to zero, and a standard deviation equal to 1, and the z-scores are given by:

`z=(x-\mu)/(\sigma)`

Where

• x is the raw value. In this case, the cutoff value we need to find.

,

• μ is the population's mean. In this case, μ = 12 million dollars

,

• σ is the population's standard deviation. In this case, σ = 1.1 million dollars.

,

• z is the z-score.

2. Now, to use the cumulative standard normal distribution, we have to find the table for which these cumulative values are tabulated, and we have to associate the z value for the cumulative 20% of this distribution. Then we have:

3. Therefore, for a cumulative probability of 0.20045 (20.045%), the corresponding value for z is z = -0.84.

4. Now, to find the value for the raw value, x, we have to solve the following equation for x as follows:

`\begin{gathered} -0.84=(x-12)/(1.1) \\ \\ -0.84(1.1)=x-12 \\ \\ -0.84(1.1)+12=x \\ \\ x=11.076 \end{gathered}`

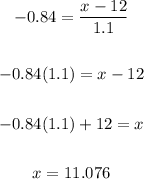
5. And we can see that 11.076 million is the cutoff between quarters that are considered "failures" by that company and quarters that are not, and we can check this in the following graph:

Therefore, if we round our answer to one decimal place, we have that 11.1 million dollars are the cutoff between quarters that are considered "failures" by that company and quarters that are not.

[That is, below 11.1 million dollars the quarters are considered "failures" by that company.]