To find the equation of the line shown, we need two points:
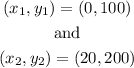
The equation of the line goes by:
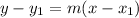
The find m, the slope, we use the formula below and find m.
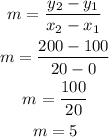
Now, let's put the point and m to find the equation:
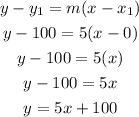
Changing to functional notation, this will be:
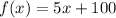
2nd answer choice is correct.