SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given equation
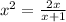
STEP 2: Simplify the equation for x
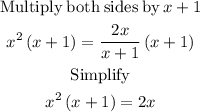
STEP 3: Solve the resulting polynomial equation

Therefore,
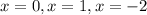
Hence, the answers will be as seen below: