Question

Find the 95% confidence interval for the standard deviation of the lengths of pipes if a sample of 11 pipes has a standard deviation of 14.6 inches

Answer 1

We use a chi-squared distribution which gives us a confidence interval that is not symmetric about the sample standard deviation.

We assume that the population of pipes is normally distributed, then

`\sqrt[]{\frac{(n-1)s^2}{\chi^{2_{}}_{\text{right}}^{}}}\le\sigma\le\sqrt[]{\frac{(n-1)s^2}{\chi^{2_{}}_{\text{left}}}}`

where s is the sample standard deviation, and sigma is the population standard deviation and n represents the sample size.

We need to find the L & R values that make

`P(L\le\chi^2\le R)=0.95`

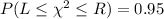
true.

Using a table or calculator, we have

`\begin{gathered} \chi^2_{\text{Right}}=20.483 \\ \chi^2_{\text{Left}}=3.247 \end{gathered}`

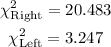
The other variables are given. Plugging all of those values in the formula, we have

`\begin{gathered} \sqrt[]{((11-1)(14.6)^2)/(20.483)}\le\sigma\le\sqrt[]{((11-1)(14.6)^2)/(3.247)} \\ 10.2\le\sigma\le25.6 \end{gathered}`

The 95% confidence interval for the standard deviation is approximately (10.2, 25.6).