Question

Find the slope of a line perpendicular to the line that passes through the points (5,12) (11,9)

Answer 1

Given the points:

(5, 12), (11, 9)

Let's find the slope of a line perpendicular to the line that passes through the given points.

The slope of a perpendicular line is the negative reciprocal of the slope of the original line:

`m_1m_2=-1`

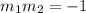
Where:

m1 is the slope of the origginal line

m2 is the slope of the perpendicular line.

To find the slope of the original line, apply the slope formula:

`m=(y2-y1)/(x2-x1)`

Thus, we have:

(x1, y1) ==> (5, 12)

(x2, y2) ==> 11, 9

`\begin{gathered} m=(9-12)/(11-5) \\ \\ m=(-3)/(6) \\ \\ m=-(1)/(2) \end{gathered}`

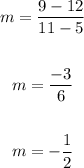
The slope of the original line is -1/2.

To fine the slope of the perpendicular line substitute -1/2 for m1 in the equation (m1m2 = -1).

Thus, we have:

`\begin{gathered} m_1m_2=-1 \\ \\ -(1)/(2)m_2=-1 \\ \\ Multiply\text{ both sides by 2:} \\ -(1)/(2)m_2*2=-1*2 \\ \\ -1m_2=-2 \end{gathered}`

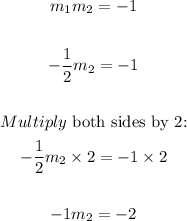
Divide both sides by -1:

`\begin{gathered} -(1m_2)/(-1)=(-2)/(-1) \\ \\ m=2 \end{gathered}`

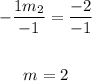
Therefore, the slope of the perpendicular line is = 2

ANSWER: