2 Answers

Jim Kennedy · Answer 1 · 2023-12-15T11:57:15+0000

Given:

The potential across the battery is

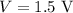
$V=1.5\text{ V}$

The resistance of each bulb in series is

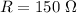
$R=150\text{ }\Omega$

To find:

The voltage between points B and C

Explanation:

The equivalent resistance of the bulbs is,

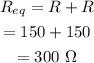
$\begin{gathered} R_(eq)=R+R \\ =150+150 \\ =300\text{ }\Omega \end{gathered}$

The current in the circuit is,

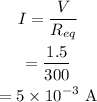
$\begin{gathered} I=(V)/(R_(eq)) \\ =(1.5)/(300) \\ =5*10^(-3)\text{ A} \end{gathered}$

The voltage drop across B and C is the same as the voltage drop across the first bulb, which is,

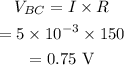
$\begin{gathered} V_(BC)=I* R \\ =5*10^(-3)*150 \\ =0.75\text{ V} \end{gathered}$

Hence, the required voltage drop is 0.75 V.

Please log in or register to add a comment.