Question

Blake is going to invest $ 34,000 and leave it in an account for 9 years . Assuming the interest is compounded annually , what interest rate , to the nearest tenth of a percent , would be required in order for Blake to end up with $ 50,000 ?

Answer 1

r = 4.4%

Step-by-step explanation:

Principal = P = $34,000

time = t = 9 years

rate = ?

FV = future value = $50,000

n = number of times compounded in a year = 1

Using the compound interest formula:

`\begin{gathered} FV=P(1+r/n)^(nt) \\ \end{gathered}`
`\begin{gathered} 50000\text{ = 34000(1 + }(r)/(1))^9 \\ 50000=34000(1+r)^9 \\ (50000)/(34000)=(1+r)^9 \end{gathered}`
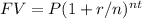
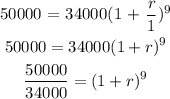
`\begin{gathered} 1.4706=(1+r)^9 \\ \sqrt[9]{1.4706}\text{ = 1 + r} \\ 1.0438\text{ = 1 + r} \\ \end{gathered}`
`\begin{gathered} 1.0438\text{ - 1 = r} \\ r\text{ = 0.0438} \end{gathered}`

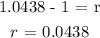
rate = 4.38%

To the nearest tenth of a percent, r = 4.4%