Question

Solve for the indicated variable in the parenthesis 2 and 4

Answer 1

`\begin{gathered} 2)\text{ W = }\frac{A\text{ - 2L}}{2} \\ 4)\text{ y = }\frac{2x\text{ -8 }}{3} \end{gathered}`

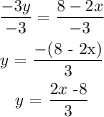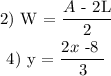
Step-by-step explanation:

2) A = 2(L + W)

We need to make W the subject of formula.

Expanding the parenthesis:

A = 2L + 2W

subtract 2L from both sides:

A - 2L = 2W

divide both sides by 2:

`\begin{gathered} \frac{A\text{ - 2L}}{2}\text{ = }(2W)/(2) \\ W\text{ = }\frac{A\text{ - 2L}}{2} \end{gathered}`

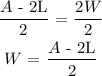
4) 2x - 3y = 8

We need to make y the subject of formula

To do this, we'll subtract 2x from both sides:

2x - 2x - 3y = 8 - 2x

-3y = 8 - 2x

Divide both sides by -3:

`\begin{gathered} (-3y)/(-3)=(8-2x)/(-3) \\ y\text{ = }\frac{-(8\text{ - 2x)}}{3} \\ y\text{ = }\frac{2x\text{ -8}}{3} \end{gathered}`