Question

Peter and John are pulling a box. Peter pulls with 120 N of force at 30° & John pulls with 100 N of force at 45°. What is the combined force (resultant) and its direction? Please calculate by algebraic method.

Answer 1

`\begin{gathered} F=174.96N \\ \theta=-3.5\degree \end{gathered}`

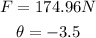
Step-by-step explanation

We want to find the resultant of the combined force and its direction.

To do this, we have to find the horizontal and vertical components of the total force acting on the box.

The horizontal component of the force is:

`\begin{gathered} F_x=120\cos 30+100\cos 315 \\ F_x=103.92+70.71 \\ F_x=174.63N \end{gathered}`

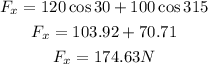
The vertical component of the force is:

`\begin{gathered} F_y=120\sin 30-100\sin 45 \\ F_y=60-70.71 \\ F_y=-10.71N \end{gathered}`

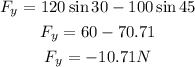
The resultant of the force can be found by using the formula:

`F=\sqrt[]{(F_x)^2+(F_y)^2}`

Therefore, we have that:

`\begin{gathered} F=\sqrt[]{(174.63)^2_{}+(-10.71)^2} \\ F=\sqrt[]{30495.6369+114.7041} \\ F=\sqrt[]{30610.341} \\ F=174.96N \end{gathered}`

To find the direction, we have to apply the formula:

`\theta=\tan ^(-1)((F_y)/(F_x))`

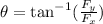
Therefore, we have:

`\begin{gathered} \theta=\tan ^(-1)((-10.71)/(174.63)) \\ \theta=\tan ^(-1)(-0.0613) \\ \theta=-3.5\degree \end{gathered}`

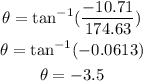
The resultant force acts 3.5 degrees below the x axis.