Question

These cylinders are similar. Find the surfacearea of the smaller cylinder. Round to thenearest tenth.5 cm13 cmSurface Area = [? ] cm2Surface Area = 236 cm2

Answer 1

The two cylinders are simillar then ratio of the surface area is equal to the ratio of the square of height.

`\begin{gathered} (s)/(S)=((3)^2)/((5)^2) \\ s=(9)/(25)S \end{gathered}`

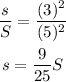
Here, s is surface area of small cylinder and S is surface area of larger cylinder.

Substitute 236 for S in the equation to determine the surface area of small cylinder.

`\begin{gathered} s=(9)/(25)\cdot236 \\ =84.96 \\ \approx85.0 \end{gathered}`

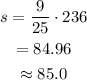
So answer is Surface Area = 85.0 cm^2.