Question

Hello, I need some help with this precalculus question for my homework, please HW Q16

Answer 1

we have the function

`A(t)=A_0*e^(-0.0244t)`

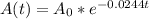
Convert into an equivalent function of the form

`y=a(b)^t`

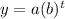
so

`A(t)=A_0e^(-0.0244t)=A_0(e^(-0.0244))^t=A_0(0.9759)^t`

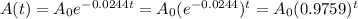
therefore

the equivalent function is

`A_0=A_0(0.9759)^t`

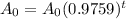
The rate of decay is equal to

b=1-r

b=0.9759

r=1-b

r=1-0.9759

r=0.0241

The answer Part a is -0.0241 (which is negative because is a decay rate)

Part b

For t=10 years

A_0=500 grams

substitute

`\begin{gathered} A(t)=500*e^(-0.0244*(10)) \\ A(t)=392\text{ grams} \end{gathered}`

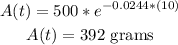
The answer part b is 392 grams

Part c

For A(t)=200 grams

Find out the value of t

substitute given values

`\begin{gathered} 200=500e^(-0.0244(t)) \\ (200)/(500)=e^(-0.0244(t)) \end{gathered}`

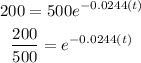
Apply ln on both sides

`\begin{gathered} ln(200)/(500)=lne^(-0.0244(t)) \\ \\ ln(2)/(5)=-0.0244t \end{gathered}`

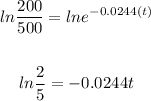
t=37.6 years

The answer part c is 37.6 years

Part d

For A(t)=A_0/2

substitute

`\begin{gathered} (A_0)/(2)=A_0e^(-0.0244(t)) \\ (1)/(2)=e^(-0.0244(t)) \end{gathered}`

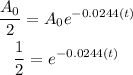
Apply ln on both sides

`ln(1)/(2)=lne^(-0.0244(t))`

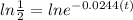
t=28.4 years

The answer part d is 28.4 years