We have 4 even numbers which sum is equal to -12.
We can write the even numbers as 2n, 2(n+1) 2(n+2) and 2(n+3), where the index n is an integer.
If we add them, we get:
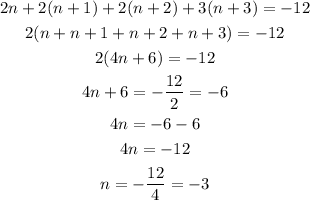
As we have find the value of n, we can replace it in the definition of the integers, and find which ones satisfy the condition:
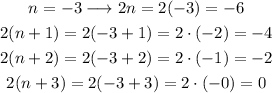
Answer: The numbers are: -6,-4,-2 and 0.