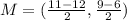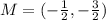For this problem we can use the definition of euclidean distance given by:
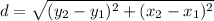
We have these coordinates:
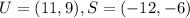
And replacing we got:
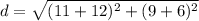
And when we simplify we got:
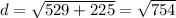
And if we simplify we got:
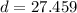
The midpoint can be calculated with this formula:
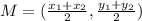
And replacing we got: