Question

How Do I solve this question? Grade 10 MJ 2020 Q4

Answer 1

We need to find the least possible value of a and the greatest possible value of b.

We know that the curve:

`y=x³-2x²+4x-9`

has no stationary points in the interval a < x

This means that y'(x) ≠ 0 for any x in the interval between a and b.

Thus, first, let's find the points where y'(x) = 0:

`\begin{gathered} y^(\prime)(x)=0 \\ \\ 3x²-2\cdot2x+4=0 \\ \\ 3x²-4x+4=0 \\ \\ x=(-(-4)\pm√((-4)²-4(3)(4)))/(2(3)) \\ \\ x=(4\pm√(-32))/(6) \end{gathered}`

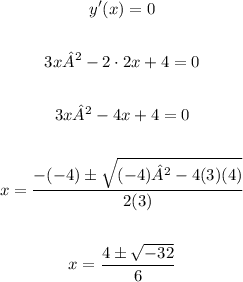
Since the values of x for which y'(x) = 0 are imaginary, there are no real values of x at which the given curve is stationary.

Therefore, a and b can be any real number.

Answer:

The minimum value of a is represented by -∞, and the maximum value of b is represented by ∞.