Question

Drag each length to the correct location on the triangle. Each length can be used more than once, but not all lengths will be used.What are the missing side lengths for the triangle?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about right isosceles triangles.

Given the following triangle:

Notice this triangle has angles 90º, 45º and 45º, hence it is a right isosceles triangle.

In fact, when the angles are equal, the opposite sides to these angles have the same measure, which means that we'll get the measure for side B as

`5√(2)`

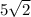
Now, to find the measure of side A, we simply apply the Pythagorean theorem, that says

For a right triangle with legs measuring a and b and hypotenuse measuring c, the sum of the squares of a and b is equal to the square of c,

`a^2+b^2=c^2`

In our case, a = b = 5sqrt(2), hence

`\begin{gathered} (5√(2))^2+(5√(2))^2=c^2 \\ \\ 50+50=c^2 \\ \\ 100=c^2 \\ \\ c=10 \\ \\ \end{gathered}`

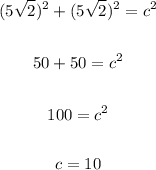
Therefore the length of the side A measures 10.