1 Answer

Jacob Franklin · Answer 1 · 2023-12-10T03:33:56+0000

$\operatorname{\pm}1,\operatorname{\pm}(1)/(2),\operatorname{\pm}2,\operatorname{\pm}4,\operatorname{\pm}8$

1) We need to use the Rational Roots Theorem:

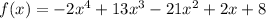
$f\mleft(x\mright)=-2x^4+13x^3-21x^2+2x+8$

So, let's write out a ratio with the possible rational roots, considering the constant term and the leading coefficient:

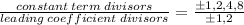
$(constant\:term\:divisors)/(leading\:coefficient\:divisors)=(\pm1,2,4,8)/(\pm1,2)$

a) So the list of all possible zeros is:

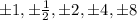
$\pm1,\pm(1)/(2),\pm2,\pm4,\pm8$

Note that "possible' does not mean the list of all real rational roots. We'd need to plug into the function and check

Please log in or register to add a comment.