Question

The equation for the height (in meters) of a ball y = -4.9x2 +*+100, where x represents time (in seconds) after the ball is thrownApproximately when will the ball hit the ground?

Answer 1

The equation is given as

`y=-4.9x^2+x+100`

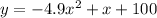
where y is the height and x is the time.

Note that at the point when the ball hits the ground, the height is 0.

Therefore, we equate y to 0, such that

`\begin{gathered} y=0 \\ \therefore \\ -4.9x^2+x+100=0 \end{gathered}`

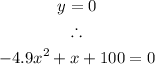
Solving the quadratic equation using the quadratic formula,

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where

a = -4.9

b = 1

c = 100

Substituting into the equation, we have

`\begin{gathered} x=\frac{-1\pm\sqrt[]{1^2-(4*\lbrack-4.9\rbrack*100)}}{2*1} \\ x=\frac{-1\pm\sqrt[]{1+1960}}{2} \\ x=\frac{-1\pm\sqrt[]{1961}}{2} \\ x=(-1\pm44.28)/(2) \end{gathered}`

Therefore, the value can be

`\begin{gathered} x=(-1+44.28)/(2) \\ x=21.64 \end{gathered}`

or

`\begin{gathered} x=(-1-44.28)/(2) \\ x=-22.64 \end{gathered}`

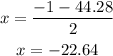
Since the time can only be positive, the time it takes for the ball to hit the ground is 21.64 seconds.