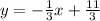The line is perpendicular to the equation:
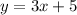
So our slope will be the negative reciprocal of the slope of this line so the new slope will be:
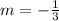
Now with the slope we can find the intercept in the y axis with the slope equation:
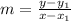
So we replace the slope and the coordinate, and replace x=0 to find the intercept so:
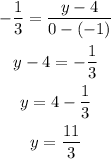
So the general equation will be: