Question

A 1670 kg car is traveling with a speed of 15 m/s. What is the magnitude of the horizontal net force that is required to bring the car to a halt in the distance of 57 meters?

Answer 1

Given data

*The given mass of the car is m = 1670 kg

*The given initial speed of the car is u = 15 m/s

*The given distance is s = 57 m

*The final speed of the car is v = 0 m/s

The formula for the acceleration of the car is given by the kinematic equation of motion as

`a=(v^2-u^2)/(2s)`

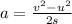
Substitute the known values in the above expression as

`\begin{gathered} a=((0)^2-(15)^2)/(2*57) \\ =-1.97m/s^2 \end{gathered}`

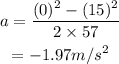
The formula for the net force that is required to bring the car to a halt in the distance of 57 meters is given as

`f_(net)=ma`

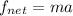
Substitute the known values in the above expression as

`\begin{gathered} f_(net)=(1670)(-1.97) \\ =-3289.9\text{ N} \\ \approx-3290\text{ N} \end{gathered}`

Here the negative sign indicates that the force is opposing the direction of motion. Hence, the magnitude of the net force is f_net = 3290 N