Question

A rectangle is inscribed in a circle with diameter 8cm. Find the dimensions of the rectangle such that the area would be a maximum.

Answer 1

Step 1. We need to find the maximum area of a rectangle inscribed in a circle.

The diameter of the circle is:

`\begin{gathered} Diameter: \\ d=8cm \end{gathered}`

Step 2. The radius of the circle is:

`\begin{gathered} Radius: \\ r=d/2 \\ r=8cm/2 \\ r=4cm \end{gathered}`

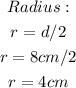
Step 3. The formula to find the maximum area of a rectangle inscribed in a circle with radius r is:

`\begin{gathered} Area: \\ A=2r^2 \end{gathered}`

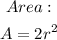
Step 4. Substituting the known value of r and finding the area:

`\begin{gathered} A=2(4cm)^2 \\ \downarrow\downarrow \\ A=2(16cm^2) \\ \downarrow \\ A=32cm^2 \end{gathered}`

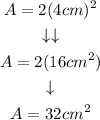
The maximum area is 32cm^2.

Step 5. The maximum area of a rectangle or quadrilateral inside a circle happens when the sides of the quadrilateral are equal. This means the quadrilateral is a square.

For a square the area formula is:

`A=l^2`

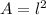
Where l is the length.

Step 6. Substituting the area to find the length of the sides:

`\begin{gathered} 32cm^2=l^2 \\ l=√(32cm^2) \\ l=4√(2)cm \end{gathered}`

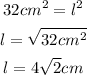
Thus, the dimensions are:

`4√(2)cm*4√(2)cm`

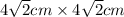
Answer: The figure for which the area is maximum is the square, and the dimensions are:

`4√(2c)m*4\sqrt[]{2}cm`