First, notice that we can write sec(A) like this:
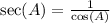
then, given the information on the problem, we have the following:
![\begin{gathered} \sec (A)=\frac{\sqrt[]{65}}{7} \\ \Rightarrow(1)/(\cos (A))=\frac{\sqrt[]{65}}{7} \\ \Rightarrow\cos (A)=\frac{7}{\sqrt[]{65}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8w2k13z1xrjbnt6b668q8jma82vi7iy86q.png)
We also know that the cosine of an angle is defined as the opposite side divided by the hypotenuse of a right triangle. We can see this in the following picture:
then, we can find the missing side using the pythagorean theorem:
![\begin{gathered} (\sqrt[]{65})^2=x^2+(7)^2 \\ \Rightarrow x^2=65-(7)^2=65-49=16 \\ \Rightarrow x=\sqrt[]{16}=4 \\ x=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/84sl9ypt5wnrwh8p0xp04m9x1zo05p7nwg.png)
now that we found the measure of the opposite side of angle A,we can calculate the sine of A to get:
![\sin (A)=\frac{\text{opposite side}}{hypotenuse}=\frac{4}{\sqrt[]{65}}](https://img.qammunity.org/2023/formulas/mathematics/college/k2ohe1uptvmxjzbsda188qf0f4hn1jgu7r.png)
then, we have the following property:
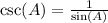
thus, using the value that we found for sin(A), we have:
![\csc (A)=(1)/(\sin (A))=\frac{1}{\frac{4}{\sqrt[]{65}}}=\frac{\sqrt[]{65}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/d3tu0wf6u6ldjrazeffbb81ni4kja0abkb.png)
therefore, csc(A)=sqrt(65)/4