Question

suppose $600 is invested at an annuak intrest rate of 4% compounded continuously. what is the amount in the account after 9.5 years

Answer 1

We are asked about the amount after 9.5 years of a continuously compounded interest rate of 4%. the formula for the continuously compounded interest rate is the following:

`A=Pe^(rt)`

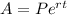
Where "r" is the interest rate in decimal notation and "t" the time. Replacing the given values we get:

`A=600e^((0.04)(9.5))`

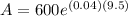
Solving the operations:

`A=600e^(0.38)`
`A=(600)(1.46)=877.37`

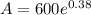
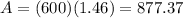
Therefore, after 9.5 years there are $877.37