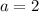Question

G(x)=|-2x|-3 Describe the transformations from f(x) = |x| to g(x)

Answer 1

Given the Parent Function (the simplest form) of Absolute Value Functions:

`f\mleft(x\mright)=|x|`

And the function obtained after the transformation:

`g\mleft(x\mright)=|-2x|-3`

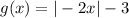
You need to remember the following Transformation Rules for Functions:

1. If:

`f(x)-k`

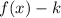
The function is shifted down "k" units.

2. If:

`f(-x)`

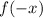
The function is reflected across the y-axis.

See the graph attach below:

Where the green function is the Parent Function and the purple function is the function g(x).

By definition, for Absolute Value functions, when the transformation is:

`f(x)=a|x|`

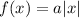
and:

`a>1`

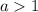
The graph is stretched.

Therefore, you can determine that the answer is:

-Translation of 3 units down.

- Reflection across the y-axis.

- Stretched by a scale factor of:

`a=2`