Answer:
17.797 m/s
Step-by-step explanation:
We can calculate the velocity of the car using the following equation:
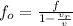
Where fo is the perceived frequency, f is the emitted frequency, vr is the speed of the car and v is the speed of the sound. So, replacing f = 2010 Hz, fo = 2120 Hz, and v = 343 m/s, we get:
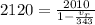
Solving for vr, we get:
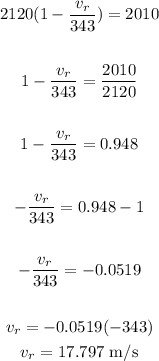
Therefore, the police car is driving at 17.797 m/s