Question

Deb Cook is given the choice of two positions, one paying $3,000 per month and the other paying $2,100 per month plus a 5% commission on all sales made during the month. What amount must she sell in a month for the second position to be more profitable?

Answer 1

the second option is more profitable

if she sells more than $ 18000 per month

Step-by-step explanation

Step 1

let's check the options we have

a)

one paying ​$3,000 per month

it means, in a month , she will receive 3.000

`\text{Option}_1=3000`

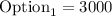
b)$2,100 per month plus a​ 5% commission on all sales made during the month

if x represents the sales, then the formula would be

`\begin{gathered} \text{Option}_2=2100+5\text{ \%(sales)} \\ \text{replacing} \\ \text{Option}_2=2100+0.05x \end{gathered}`

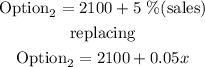
Step 2

now, to make the option 2 more profitable

`\begin{gathered} \text{option}_1\leq option_2 \\ 3000\leq2100+0.05x \\ \end{gathered}`

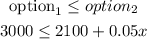
solve for x

`\begin{gathered} 3000\leq2100+0.05x \\ subtract\text{ 2100 in both sides} \\ 3000-2100\leq2100+0.05x-2100 \\ 900\leq0.05x \\ \text{divide both sides by 0.05} \\ (900)/(0.05)\leq(0.05)/(0.05)x \\ 18000\leq x \end{gathered}`

therefore, the second option is more profitable

if she sells more than $ 18000 per month

I hope this helps you