Consider the general case

This equation has the solutions
![x=\frac{-b\text{ }\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/6ztpowwc16vzvwajrs0c3uc65wwqv9o26z.png)
In here, the quantity
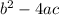
is called the discriminant. If the discriminant is greater than or equal to zero, then the roots of the equation are real. If the discriminant is negative, the roots are imaginary (complex roots).
In our case 5x^2-7x+12, a=5,b=-7,c=12. Then, the discrimininant is
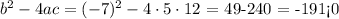
This means that the roots of this equation are all imaginary (complex).