Question

6b) Find the X value for each of the following z-scores.z = -1.00z = 0.75z = 0.50z = -1.25z = -1.50z = 2.60

Answer 1

• z=-1.00, X=70

,

• z=0.75, X=105

,

• z=0.50, X=100

,

• z=-1.25, X=65

,

• z=-1.50, C=60

,

• z=2.60, X=142

Explanation:

Given a sample whose:

• Mean = 90

,

• Standard Deviation = 20

To find the X-values from the given z-scores, we use the formula below:

`X=z\sigma+\mu\text{ where }\begin{cases}{z=z-score} \\ {\mu=mean} \\ {\sigma=Standard\;Deviation}\end{cases}`

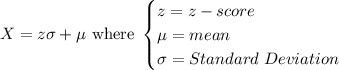
(a)z=-1.00

`X=-1.00(20)+90=70`

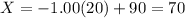
The X-value is 70.

(b)z=0.75

`X=0.75(20)+90=15+90=105`

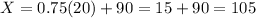
The X-value is 105.

(c)z=0.50

`X=0.50(20)+90=10+90=100`

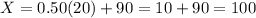
The X-value is 100.

(d)z=-1.25

`X=-1.25(20)+90=-25+90=65`

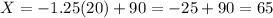
The X-value is 65.

(e)z=-1.50

`X=-1.50(20)+90=-30+90=60`

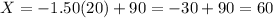
The X-value is 60.

(e)z=2.60

`X=2.60(20)+90=52+90=142`

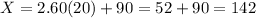
The X-value is 142.