The expected winnings are given by the following formula:
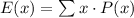
were x all the gains and P(x) their individual probabilities.
Then, the probability of getting a 6 is 1/6, the probability of getting a 5 is 1/6 and the probability of getting a 4 is 1/6, then the expected winnings for this game are:
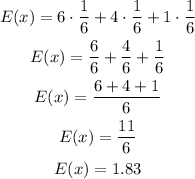
The expected winnings are $1.83.