To find slope, we can use the formula:

Where

are the 2 points the line goes through.
All the 3 dotted lines have the same slope. We can use any of the dotted lines. Let's use the top-most one.
The 2 point it passes through are:
(0,8) and (2,7)
Thus, the slope would be:
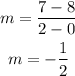
To find the slope of reflection line, we take 2 points on the line and follow the same process.
The two points on the reflection line are:
(0,3) and (1,5)
Thus, the slope would be:
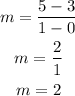 Slope of Dotted Line(s): -1/2Slope of Reflection Line: 2
Slope of Dotted Line(s): -1/2Slope of Reflection Line: 2