Question

A random sample of size n is required to produce a margin of error of +/- E. By what percent does the sample size need to increase to reduce the margin of error to +/- 9/10E? Round your answer to the nearest percent

Answer 1

The margin of error is inversely proportional to the square root of the sample size. We know that for a certain sample size n, the margin of error is +/- E, thus:

`E=(k)/(√(n))`

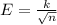
Where k is the constant of proportionality.

We need to know the sample size N that produces a margin of error of +/-9/10E:

`(9)/(10)E=(k)/(√(N))`

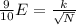
Substituting the value of E from the first equation:

`(9)/(10)(k)/(√(n))=(k)/(√(N))`

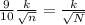
Simplifying by k:

`(9)/(10)(1)/(√(n))=(1)/(√(N))`

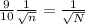
Squaring and solving for N:

`\begin{gathered} (81)/(100)(1)/(n)=(1)/(N) \\ \\ N=(100)/(81)n \end{gathered}`

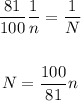
We need to calculate the percentage of increase of n to get N. Subtracting n:

`N-n=(19)/(81)n`

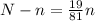
Dividing by n:

`(N-n)/(n)=(19)/(81)`

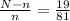
The sample size must be increased by 19/81 = 0.2346.

It's equivalent to 23% (rounding to the nearest percent)

Answer. 23%