From the problem, the distance travelled is 720 miles.
Let 2x be the speed of the corporate jet
and
x be the speed of the smaller plane, since smaller plane can fly half as fast as the corporate jet.
Let y be the travel time of the corporate jet
and 6 - y be the travel time of the smaller plane since the total time is 6 hours
The working equation is :
speed x time = distance
For the corporate plane :
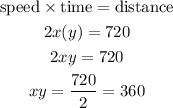
For the smaller plane :
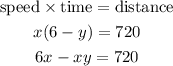
Substitute xy = 360 to the 2nd equation :
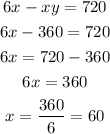
x = 60 which is the speed of the smaller plane
The speed of the corporate plane will be :
2x = 2(60) = 120
The answer :
corporate jet = 120 mph
smaller plane = 60 mph